哈密頓算子 (Hamiltonian) 對應量子系統的總能量，而我們想要模擬時間演化算子 (time evolution operator) 以便計算出經過時間 之後的量子態。換句話說，給定初始態 ，我們想要知道 。

對於任意的 Hamiltonian ， 不容易計算，常見的逼近方法是 Lie-Suzuki-Trotter methods。在 QSVT 的框架中，我們首先假設 的特徵值都是正的，於是 的奇異值和特徵值相等 (這個假設可以避免，但在此省略)。接著，觀察到

也就是說計算 相當於，先計算 和 然後相加！我們可以利用 QSVT 各別計算出 和 ，但是要如何相加？在量子計算中，每多應用 (apply) 一個量子閘 就是將原本的量子態「乘上」​，但是要進行相加操作，我們需要使用名為 Linear Combination of Unitaries (LCU) 的方法。LCU 善用了 Hadamard transformation 和 controlled gate 的特性來達成么正矩陣相加的效果，詳情請見 QCnote 第九章。以上基於 QSVT 的 Hamiltonian simulation 方法可以下圖總結 (圖來源：A Grand Unification of Quantum Algorithms)：

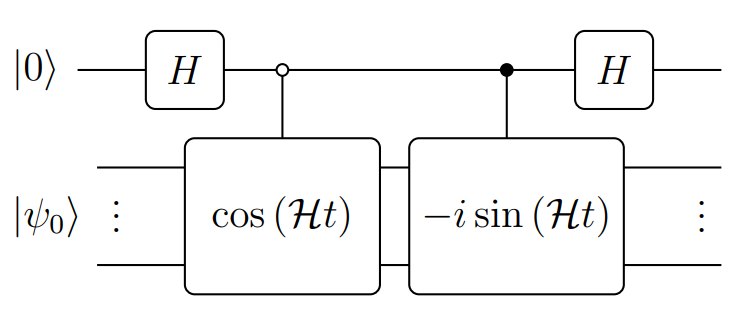
值得注意的是，基於 QSVT 的 Hamiltonian simulation 方法在 query complexity 方面是「最佳的」(optimal)！(事實上，QSP 本身就能做到 optimal Hamiltonian simulation！，請參閱這篇)

不知不覺談了快要 20 天的理論，明天就來實作一下吧！

參考資料

• A Grand Unification of Quantum Algorithms
• Optimal Hamiltonian Simulation by Quantum Signal Processing (arxiv.org)